Customer Segmentation EDA

Marketing campaigns play a crucial role in promoting products and services, and understanding the behavior of customers is essential for designing effective strategies. In this post, I conduct an Exploratory Data Analysis (EDA) on a marketing campaign dataset. The goal is to gain insights into customer behavior and uncover patterns that can inform marketing strategies. 

The dataset we'll be working with is sourced from Kaggle (link: Marketing Campaign Dataset). It provides valuable information about customer interactions with marketing campaigns, offering an opportunity to understand their characteristics, preferences, and shopping behaviors.

In this analysis, I clean the data, reduce its dimensionality with PCA algorithm, cluster similar customers using K-Means algorithm, and identify common characteristics within each cluster.

By the end of this EDA, my goal is to discover actionable insights that can help develop personalized marketing strategies and enhancing customer engagement. Let's delve into the details of the exploratory analysis, and discover the valuable information hidden within this marketing campaign dataset.

Read More

Principal Components Analysis Algorithm

Principal Component Analysis (PCA) is one of the most famous models used for dimensionality reduction. It uses an orthonormal transformation to convert a set of observation of possibly correlated variables into a set of linearly uncorrelated variables. It corresponds to a feature extraction technique, which means that instead of selecting a subset of the original features, these methods transform the original features into a new set of features with reduced dimensionality,  in Dimensionality Reduction and Feature Extraction you can read more about dimensionality reduction and feature extraction techniques.

Given a dataset consisting of a set of vectors (points) in a high dimensional space, the main idea of PCA is to find the directions, also called principal components, along which the points line up best and make a projection on these components to create a new reduced dataset, but capturing the most relevant information.

The PCA algorithm starts by choosing the number of principal components (number of dimensions to reduce), then the covariance matrix of the dataset is calculated, as well as the eigenvectors and eigenvalues of this matrix. The eigenvectors are used to perform the transformation and eigenvalues to choose which eigenvectors are taken. The N-eigenvectors with the highest corresponding eigenvalues (in descend order) are used as to build a transformation matrix. Finally, to obtain a low dimensional dataset with new features, the original dataset is multiplied by the transformation matrix. The whole process is described in the next image, which provides an outline of the basic PCA algorithm.

Implementing algorithm in Python

Depending on each dataset, the selection of the number of dimensions may vary. In this post we generate a 2-dimensional dataset and reduce it to a 1-dimensional dataset, but these parameters can be  easily modified to apply the PCA algorithm with different datasets.

Importing libraries

First, we import the necessary libraries for the code, which includes:

# Importing libraries
import numpy as np
from numpy.linalg import eig
from sklearn.preprocessing import normalize
from sklearn.decomposition import PCA as PCA_sklearn
from sklearn.preprocessing import StandardScaler
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt

• numpy: Provides mathematical functions for arrays, we also import the function eig to calculate eigenvalues and eigenvectors.

• sklearn: Library that contains methods for data preprocessing and machine learning models. In this post the functions imported are: StandardScaler, which standardize features by removing the mean and scaling to unit variance; normalize, that normalizes vectors to unit norm and PCA_sklearn, it provides an implementation of the PCA algorithm.

• scipy: provides algorithms for optimization, integration, statistics and many other classes of problems. In this post we imported the function multivariate_normal, it enables the generation of random samples from a multivariate normal distribution.

• matplotlib: It is  a comprehensive library for creating static, animated, and interactive visualizations

Defining Functions

We define two functions: createDataset and PCA

# Create bivariate dataset
def createDataset(cov, mean, n_points, seed = 101):
  # Defining dataset
  distr = multivariate_normal(cov = cov, mean = mean, seed = seed)
  X = distr.rvs(size = n_points)
  # Scaling dataset
  sc = StandardScaler()
  X_scaled = sc.fit_transform(X)
  return X_scaled

# PCA algorithm
def PCA(X, n_components):
  # Calculating matrix of covariance
  cov_matrix = np.cov(X.T)
  # Eigenvectors and eigenvalues
  eigenvalues, eigenvectors = eig(cov_matrix)
  sort = np.argsort(eigenvalues)[::-1]
  eigvalues_sort = eigenvalues[sort]
  # Principal Components
  eigvectors_sort = normalize(eigenvectors.T[sort], axis = 0)
  # Matrix of transformation
  transformation_matrix = eigvectors_sort.T
  # Applying transformation to original dataset
  reduced_dataset = X @ transformation_matrix[:,0:n_components]
  return reduced_dataset, eigvectors_sort

The createDataset function generates a bivariate dataset with a multivariate normal distribution, taking the following parameters: covariance matrix (determines the shape and orientation of the distribution), mean vector (specifies the center of the distribution), number of points to generate and seed for the random number generator (optional). This function also standardizes the dataset using the StandardScaler function to ensure that have zero mean and unit variance.

The PCA function takes the input dataset X and the number of components n_components as parameters. It follows the steps early explained to perform the Principal Component Analysis algorithm and returns the reduced dataset and the sorted eigenvectors (principal components).

Generating Dataset

We generate a synthetic dataset X of 350 points using the createDataset function, and also defined one as the number of components for the PCA algorithm.

# Choosing parameters
cov = np.array([[1, 0.9], [0.9, 1]])
mean = np.array([0,0])
n_points = 350
n_components = 1

# Creating dataset
X = createDataset(cov, mean, n_points)

Plotting the original dataset

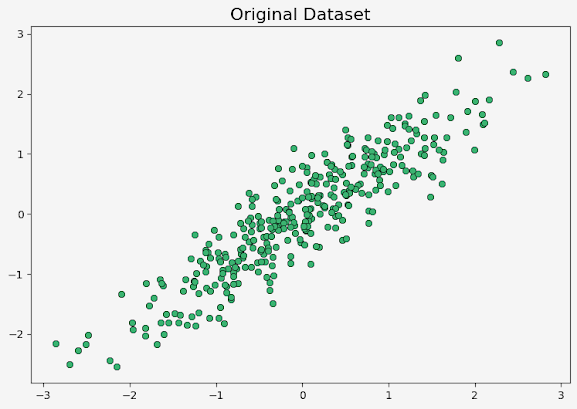
The matplotlib is used to create a scatter plot of the original dataset X. 

# Plotting original dataset
plt.rcParams['font.size'] = '10'
f, axs = plt.subplots(1,1, figsize=(7,7), facecolor='#F5F5F5')
axs.set_facecolor('#F5F5F5')
axs.plot(X[:, 0], X[:, 1],'o', c='mediumseagreen',markeredgewidth = 0.5,markeredgecolor = 'black') 
axs.set_title("Original Dataset", fontsize="16")
plt.show()

Applying PCA algorithm

Here we apply the PCA algorithm to the dataset X using the PCA function. It retains only 1 principal component (n_components). The reduced dataset and the corresponding eigenvectors are stored in the variables reduced_dataset and components, respectively.

# Applying PCA algorithm
reduced_dataset, components = PCA(X, n_components)

Another alternative is to use the PCA model from the library sklearn

# Applying PCA algorithm from sklearn
pca_sklearn =  PCA_sklearn(n_components=1)
pca_sklearn.fit(X)
reduced_dataset = pca_sklearn.transform(X)

Plotting the PCA result (reduced dataset)

We create a scatter plot to visualize the reduced dataset after applying PCA algorithm. It plots the values from the reduced dataset on the x-axis. All y-values are 0 because the dataset has only one dimension, which corresponds to x-axis in this visualization.

# Plotting PCA result (reduced dataset with only one feature)
f, axs = plt.subplots(1,1, figsize=(9,5), facecolor='#F5F5F5')
axs.set_facecolor('#F5F5F5')
axs.scatter(reduced_dataset[:,0],len(reduced_dataset)*[0],s=200, zorder = -1, color="mediumseagreen", alpha = 0.3) 
axs.set_title("Reduced dataset with only one feature", fontsize="16")
plt.show()

The result is:

Bonus: Visualizing the Principal Components

We create a scatter plot to visualize the directions of the principal components. The points of the original data set are plotted as green circles with transparency along with the two principal components as vectors (arrows), for this we use the components variable obtained from the PCA function.

# Plotting principal components
origin = np.array([[0, 0],[0, 0]]) # origin point
components_scaled = components * np.array([[1.0], [0.5]]) # scaled principal components
f, axs = plt.subplots(1,1, figsize=(7,7), facecolor='#F5F5F5')
axs.set_facecolor('#F5F5F5')
axs.scatter(X[:, 0], X[:, 1],s=50, zorder = -1, color="mediumseagreen", alpha = 0.3) 
axs.quiver(*origin, components_scaled[:,0], components_scaled[:,1], color=['mediumblue','firebrick'], scale=3, headwidth = 4, width = 0.011)
axs.set_title("Principal Components Visualization", fontsize="16")
plt.show()

By following these steps, the code generates a bivariate dataset, applies PCA, and visualizes the original dataset, principal components, and the reduced dataset.

Read More

Feature Extraction

Feature extraction techniques explore the relationships and dependencies between features to create a new dataset of transformed features. Unlike feature selection methods that only select the best features from the existing ones, feature extraction models go further by generating new features that capture the essential information of the original data. This transformed dataset not only has a lower dimensionality but also retains the interesting and intrinsic characteristics of the original data.

The goal of feature extraction is to reduce the complexity of the model by transforming the original features into a new representation that captures the most relevant information. This can lead to improved efficiency, reduced generalization error, and decreased overfitting, as the model can focus on the most informative aspects of the data.

There are different perspectives on what properties or content from the original dataset should be preserved in the transformed dataset, resulting in a wide range of feature extraction techniques. Some of the most popular feature extraction algorithms include Principal Component Analysis (PCA), Linear discriminant analysis (LDA) and Non-Negative Matrix Factorization (NMF).

Principal Component Analysis

Principal Component Analysis (PCA) is a widely used feature extraction method that aims to transform the original features into a new set of uncorrelated features called principal components. The key idea behind PCA is to capture the maximum amount of variance in the data with a reduced number of features.

PCA achieves this by finding a set of orthogonal axes, called principal components, that represent the directions of maximum variance in the data. The first principal component captures the most significant variation, followed by the second principal component, and so on.

In the above image the two principal components of a dataset are shown, easily we can identify that the amount of information in the direction of blue axis is greater than the red axis (these axes are called eigenvectors or principal components). To reduce the dimensionality of the dataset, we simply have to make a projection on the first principal components (the exact number of components is chosen by the user).

By selecting a subset of the most important principal components, PCA effectively reduces the dimensionality of the data while preserving the most significant information. PCA is particularly useful when dealing with highly correlated features or when the data is characterized by a large number of dimensions. It helps in visualizing and understanding the underlying structure of the data and can be used as a preprocessing step for various machine learning tasks.

Linear Discriminant Analysis

Linear Discriminant Analysis (LDA) is a feature extraction technique commonly used in classification tasks. Unlike PCA, which focuses on maximizing variance, LDA aims to find a linear combination of features that maximizes the separability between different classes. This is achieved by mapping the data into a lower-dimensional space while maximizing the between-class distances and minimizing the within-class variances. It finds a set of discriminant functions that maximize the ratio of between-class scatter to within-class scatter.

By projecting the data onto the derived discriminant axes, LDA creates a new feature space where the classes are well-separated, making it easier for classification algorithms to discriminate between different classes. LDA is particularly effective when there is a clear class separation in the data and can improve classification performance by reducing the dimensionality of the feature space.

Non-Negative Matrix Factorization

Non-Negative Matrix Factorization (NMF) is a feature extraction method that decomposes the original data matrix into two low-rank matrices: one representing the basis or feature vectors and the other representing the coefficients. NMF assumes that the original data can be represented as a linear combination of non-negative basis vectors.

NMF is particularly useful for data with non-negative values, such as text data or image data. It can be applied to extract meaningful components or topics from text documents or to represent images in terms of interpretable parts.

NMF iteratively updates the basis vectors and coefficients until it converges to a representation that captures the most important features of the data. The resulting low-dimensional representation can be used for various tasks, including clustering, visualization, or as input for subsequent machine learning algorithms.

Read More